[最も好ましい] 集合 数学 ���き方 286456-集合 数学 解き方
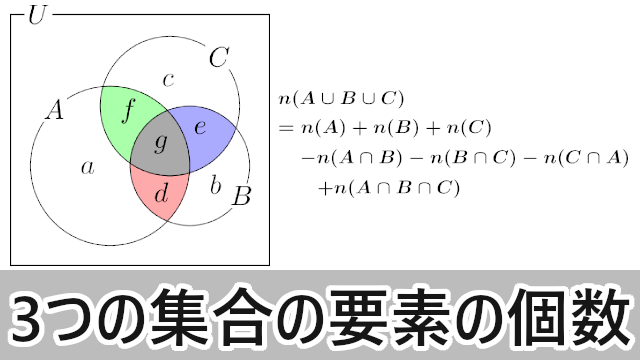
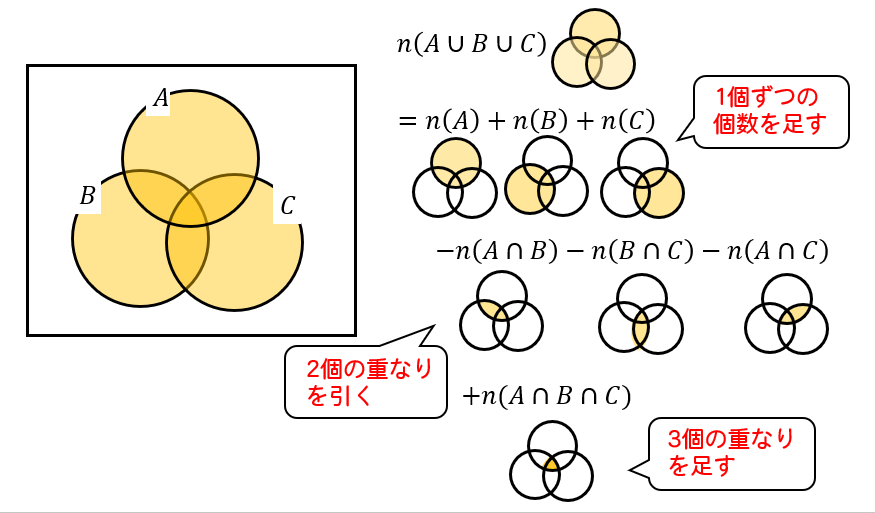
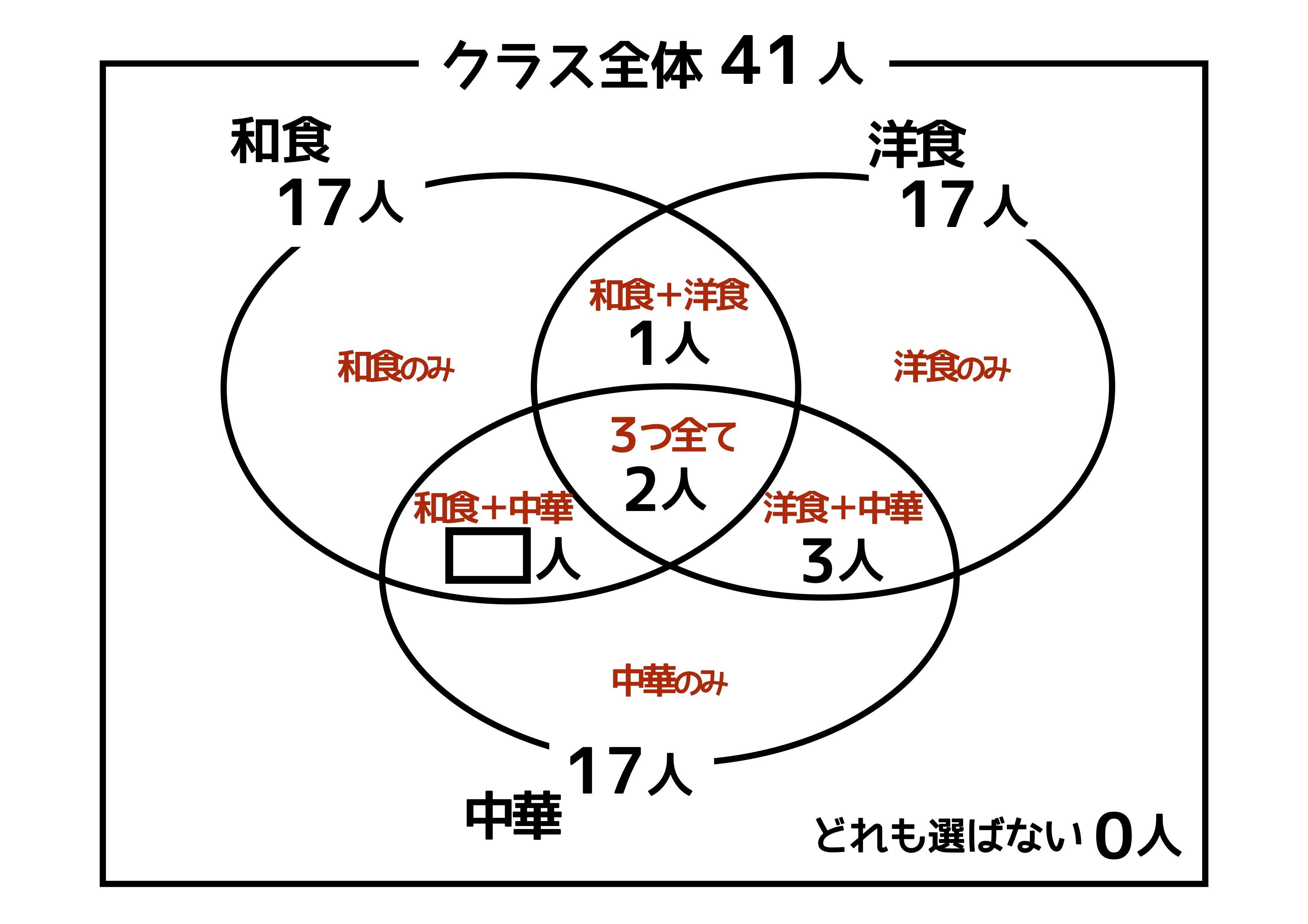
数学ia 3つの集合の要素の個数 大学入試数学の考え方と解法
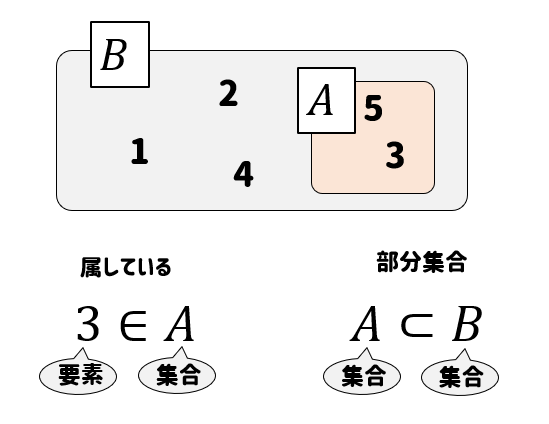
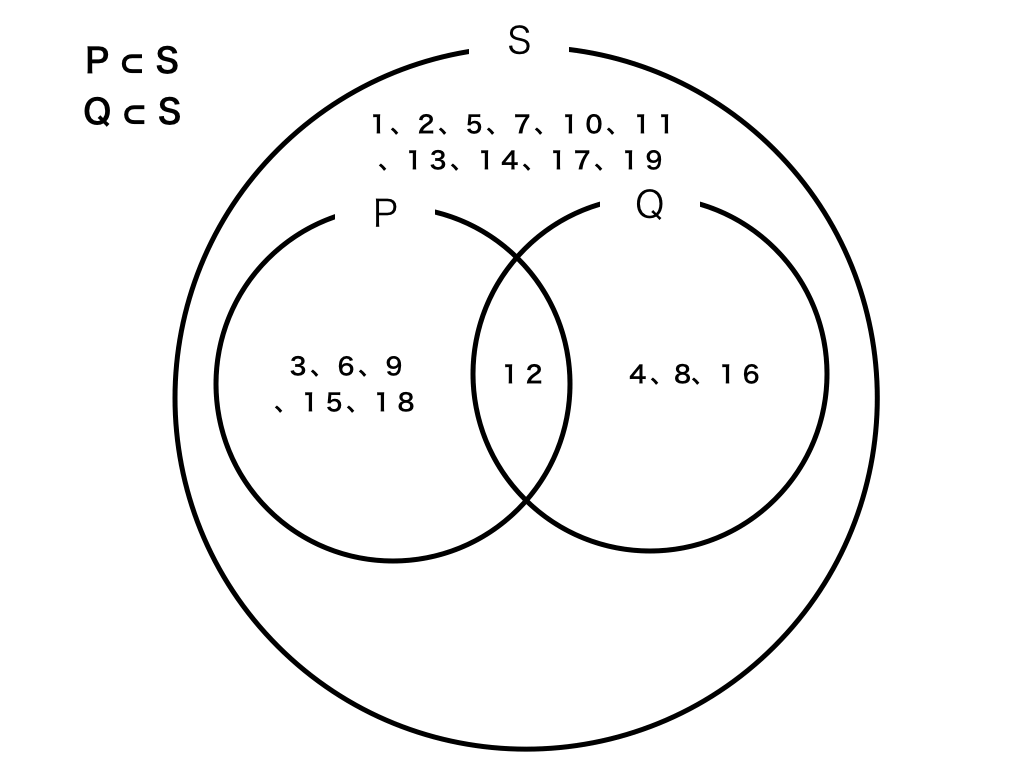
「集合 は集合 の『 部分集合 』である。 」 といいます。 記号で表すと または と表します。 要素を表すときは (左に要素)だけを使うように注意しましたので、集合のときも のように限って使うようにしておくと間違えなくて済みます。 問題にあるときは読み取れればそれで良いです。 また、 であり、かつ が分かっているとき、 「 は の『 真部分集合 』である。 」 といいます。 記号では や と書 今まで解いた問題からピックアップして、解き方の流れをまとめました*\ (^o^)/* 数学a 解法 まとめ 論理と集合 対偶 証明 必要条件 十分条件 真偽 集合と命題 命題 集合 反例 確率 数学A 図形の性質 数A この著者の他のノートを見る このノートが参考になったら、著者をフォローをしませんか? 気軽に新しいノートをチェックすることができます! コメント コメントはまだありません。 お
集合 数学 解き方
集合 数学 解き方- Unit 命題, 「今まで解いた問題からピックアップして、解き方の流れをまとめました*\(^o^)/*」, Keyword 数学a,解法,まとめ,論理と集合,対偶,証明,必要条件,十分条件,真偽,集合と命題,命題,集合,反例,確率,数学A,図形の性質,数A 行列式の求め方 行列式の求め方はかなり特殊 まず、もう既に知っていると思いますが、行列式の求め方はかなり特殊です。 恐らく皆さんの教科書には、次のような「行列式の定義」が書かれていることでしょう。

集合 必ず覚えなくてはならない6つの記号と3つの法則 高校生向け受験応援メディア 受験のミカタ
数学です。 解き方 問題文には集合によってと書かれていたのでp,qの集合をそれぞれ出して相違点を見つければいいと思うのですが、わざわざ 「18=2・3^2, 24=2^3・3であるから」 という断りを入れる必要はあるのでしょうか? 集合の範囲の記号(⊂、⊃、∩、∪、∈、∋)の読み方を教えてください! ⊂ 読み方真部分集合(しんぶぶんしゅうごう)、含む、含まれる 入力方法しゅうごう ⊃ 読み方真部 集合は記号が色々とありすぎてごっちゃになる ド・モルガンの法則ってなんだっけ? 和集合の問題はいつもミスしてしまう なんて思ったことはありませんか? 集合は学校で習うとき、要素やら部分集合やら空集合やら否定やらなんやら、新しい言葉が一気に降り掛かってくること
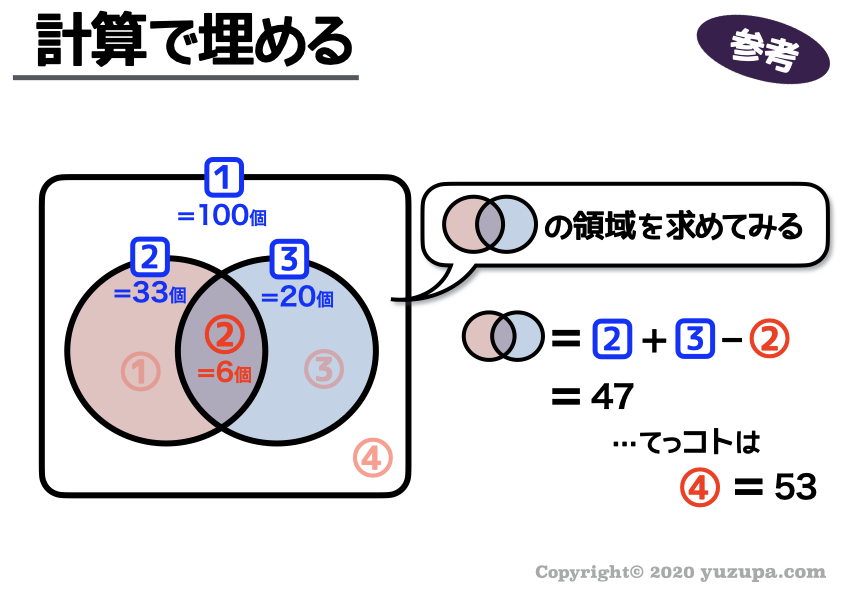
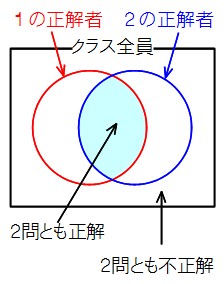
集合の解き方(1) 今日は、集合に関する問題です。 以下2問を計2分以内で解いてみましょう。 例題1: あるクラス40人に好きな科目についてのアンケートをとった。 14人の生徒は理科について嫌いで、35人の生徒は数学について嫌いといっている。 また (1)と(4)の解き方を比較してみましょう。 (1)は「2つに1つの割合だから2で割ればいい」と考えました。 この発想で(4)を解いてみると、「3つに1つの割合なので、 $0\div3=666\cdots$ という結果から、66個」と答えてしまうかもしれません。必要条件,十分条件の問題の解き方 ① 矢印で考える. 対象となるものを2つ並べて矢印を引いて考える. 覚え方: 十分な所から必要な所に流れる. (というかこれ,自然の摂理ですよね) ② 集合で考える. ベン図を描いて,どちらが広いかを考える
集合 数学 解き方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  | |
「集合 数学 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「集合 数学 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「集合 数学 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
「集合 数学 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
「集合 数学 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「集合 数学 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
「集合 数学 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「集合 数学 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「集合 数学 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「集合 数学 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「集合 数学 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |
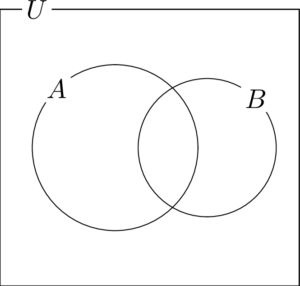
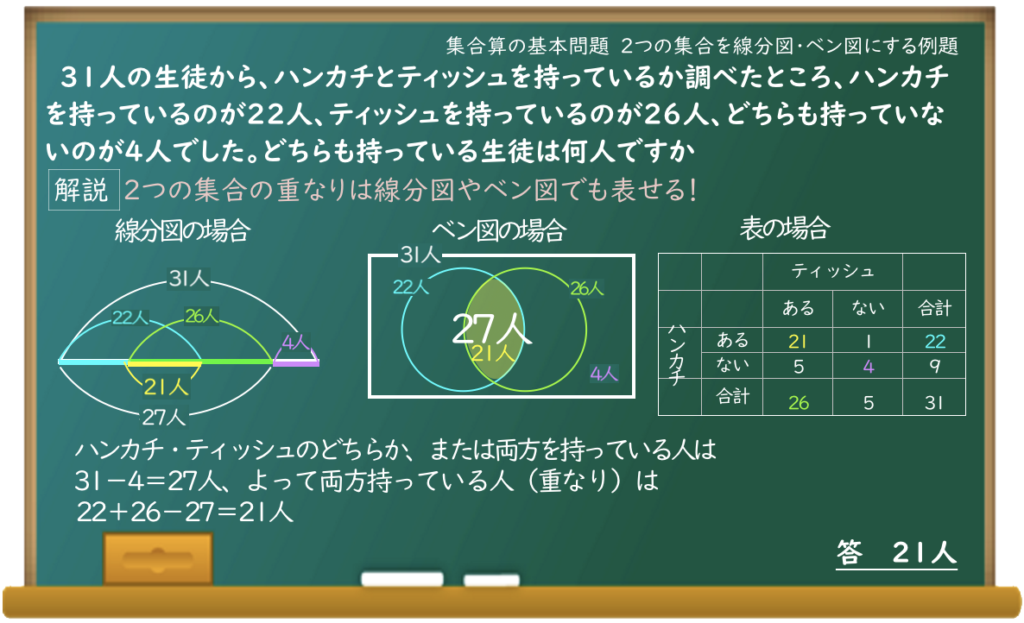
集合とは 集合の表し方 「1けたの奇数」のように、範囲がはっきりしたものの集まりを集合といいます。 集合を構成する \(1\) つ \(1\) つのものを要素といいます。 集合の表し方は、要素の満たす条件を書く方法と、要集合の要素の決定の考え方と解き方を解説! 必要十分条件の意味、覚え方をイチから解説! 逆裏対偶の作り方と意味は?? 対偶を利用した証明の解答例まとめ! 背理法による証明の解答例まとめ!
Incoming Term: 集合 数学 解き方,
コメント
コメントを投稿